VOLÚMENES DE TIERRA O TERRACERÍA

El trabajo de calcular volúmenes de tierra tiene 2 finalidades.

1. Para efecto de costeo
2. Para efecto de establecer una superficie predeterminada de cualquier obra

Que se requiera ejecutar.

El trabajo de campo consistirá en obtener toda la altimetría (curvas de nivel, perfiles, secciones transversales, terrazas, etc.) y para efecto de poder realizar dichas obras se colocan guías que pueden ser estacas, trompos con sus respectivas elevaciones.

Métodos de cubicación en terracería

La medición directa de volúmenes de tierra raras vez se efectúan en topografía,

Si no que se emplean en mediciones indirectas determinando las curvas de nivel

Y áreas que tengan relación con el volumen deseado.

Se utilizan 4 procedimientos principales

1. El método de curvas de nivel
2. El método de área base por la altura
3. El método de uso de perfiles
4. Método de usos de las secciones transversales

• MÉTODO DE CURVAS DE NIVEL

Como una alternativa para la determinación de volúmenes por medio de secciones transversales; es posible calcular el volumen usando las áreas horizontales contenidas por curvas de nivel. Los volúmenes basados en curvas de nivel se obtienen a partir de planos topográficos planímetros, para obtener las áreas se realiza por el planímetro, la superficie límite por cada curva de nivel y multiplicando el promedio de las áreas por las equidistancias entre dichas curvas de nivel.

• METODO DE AREA BASE POR ALTURA

El cálculo de un volumen por este método resulta fácil si se conoce las elevaciones de los determinados puntos que forman una figura sencilla tales como triángulos, cuadrados, rectángulos, trapecios etc.

Se puede obtener mayor precisión en terrenos abruptos utilizando áreas triangulares en vez de rectángulos. El volumen entonces es igual al área del triángulo multiplicado por el promedio de sus 3 alturas de sus vértices así: 

(si la base es un triángulo)

(Si la base es un rectángulo)

• VOLÚMENES POR ALTURA DE PUNTOS

Este método para determinar volúmenes es especialmente útil en la determinación de volúmenes para grandes excavaciones abiertas para tanques, áreas de material, etc. y para operaciones de nivelación tal como campos de juego o sitios de construcción.

Se puede aplicar también en la determinación de volúmenes de desperdicios. Habiéndose localizado la línea exterior de la estructura sobre el terreno, el Ing. o Arq. debe de dividir el área en cuadros o rectángulos, marcando las esquinas y posteriormente tomar lecturas de nivel sobre estas.

El tamaño de los cuadros dependerá de la naturaleza del terreno; las esquinas deberán estar lo suficientemente cercanas para considerar la superficie del terreno entre las líneas como un plano restando el nivel observado del correspondiente restando el nivel observado del correspondiente nivel del proyecto, se obtiene una serie de alturas de las curvas se puede determinar el volumen de cada cuadro como el área plana multiplicada por el promedio de las profundidades de excavaciones(0 rellenos) en las cuatro esquinas.

Cota de excavación de la terraza es de 714 ms en los cuadros a,b,c,d vol.

De cada prisma= hpromxarea de la base

Resolvamos este ejercicio

Prisma A diferencia de cotas
(743.1-714) +(734.8-714) +(727.3-714) +(737.2-714)
Hprom= (29.1+20.8+13.3+23.2) /4= 21.6
Prisma B
(734.8-714) +(727.3-714) +(717.4-714) +(727.3-714)
Hprom = (20.8+13.3+3.4+13.3) /4= 12.7
Prisma C
 (737.2-714) +(727.3-714) +(722.5-714) +(729.3-714)
Hprm = (23.2+13.3+8.5+15.3) /4 =15.075
Prisma D
(727.3-714) +(717.4-714) +(714.3-714) +(722.5-714)
Hpro = (13.3+3.4+0.3+8.5) /4 = 6.375

Hprom = ( 21.6 + 12.7 + 15.075 + 6.375 ) / 4 = 13.9375 mts

Existen 2 formas de calcular el volumen:

1. Encontrando el área del prisma así A = 10 x 10 = 100 mts luego el volumen así:          V= el área multiplicado por Hprom + el área multiplicado por Hprom.....                            V = 100*21.6 + 100*12.7 + 100*15.075 + 100*6.375 = 5,575
2. La otra forma es obteniendo el área así: A = 20*20 = 400 luego obtener el volumen asi:  V = al área * Hprom asi: V = 20*20*13.9375 = 5'575

• MÉTODO A TRAVÉS DE LA FRECUENCIA

Este método consiste en verificar cuántas figuras geométricas llegan a cada vértice. 
Así nivel terraza =714

Forma de anotar y poder obtener el volumen:

Hprm = ∑ prod / ∑ frecuencia

Hprm = 223. / 16 = 13.9375 mt

Vol =  hpromxArea

Vol = 13.9375x20x20

Vol = 5575 mts3

• CUANDO TENEMOS CURVAS DE NIVEL

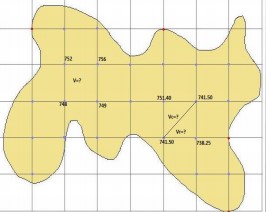
Cuando se tiene en un terreno solo las curvas de nivel y queremos calcular los volúmenes de tierra de una sección donde se piensa realizar una construcción, se tiene que realizar una interpolación para poder obtener las elevaciones del área que se va a necesitar obtener dichos volúmenes.

• MÉTODO DEL PERFIL

A partir del perfil del proyecto se hallan las profundidades promedias de las secciones transversales para la cual se mide con planímetro o con cualquier figura geométrica.

1. Condiciones para aplicar el método
2. En la sección de corte o de relleno, se considera el terreno que es de un mismo nivel.
3. La altura media se considera igual.
4. El ángulo de inclinación se considera de 45°

SECCIONES TRANSVERSALES

Donde: hc y hr seran valores promedios y constantes y b es variable así ,

hcm= altura de corte medio

De Igual Forma Cuando Es Una Sección De Relleno

EL VOLUMEN V=A*L

V RELLENO= AMR*ΣLR

V CORTE= AMC*∑LC

• CÁLCULO DE VOLÚMENES DE TIERRA

Existen varios métodos para determinar los volúmenes, el más práctico para para proyecto de carretera es aquel que se calcula entre dos secciones transversales consecutivas, multiplicando por la distancia que los separa.

EL VOLUMEN SERÁ 𝑉 = 𝐿( 𝐴1+𝐴2 /2 )

L= DISTANCIA ENTRE LAS DOS SECCIONES,

A1= ÁREA DE LAS SECCIÓN 1 A2= ÁREA DE LA SECCIÓN 2

Y CUANDO LAS DOS SECCIONES TIENDEN A CERO EL VOLUMEN SE CALCULA ASI: 

𝑉 = 1 3 ∗ 𝐴 ∗ L

• MÉTODOS DE LAS ÁREAS MEDIAS

(Las dos secciones en corte o relleno)

CÁLCULO DE VOLÚMENES DE TIERRA

Cuando deseamos una mayor precisión o el valor de las 2 áreas el valor de las 2 áreas es muy diferente entre sí, se calcula el volumen como si fuera un prismoide así:

𝑉𝑜𝑙 = 𝐿 6 ∗ (𝐴1 + 4𝐴𝑚 + 𝐴2)

AM = ÁREA MEDIA. Pero Cuando Solo Tenemos Los Promedios Se Le Puede Corregir Por LA Fórmula De La Corrección Así: 𝐶 = 1.68(𝐻𝑜 − 𝐻1) (𝐷𝑜 − 𝐷1)

DONDE C = CORRECCIÓN PARA UN PRISMOIDE.

Ejemplo a resolver: calcular el volumen entre las dos secciones aplicando los métodos. Distancia entre estaciones es de 20 mts. 

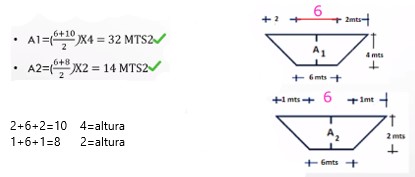
1. Fórmula de los promedios 
2. Formula del prismoide 
3. Fórmula por corrección.

SOLUCION:

Ejemplo a resolver: Calcular el volumen entre las dos secciones aplicando los metodos. Distancia entre estaciones es de 20 mts

NOTA: Fórmula del prismoide L= distancia entre estaciones es de 20mts 

Formula por correccion: Altura1=4 Altura2=2  D1= 2+6+2=10 D2=1+6+1=8

Ajustar cálculos: 460 es de la formula de los promedios y el 6.72 de la formula por correccion.

BIBLIOGRAFÍA:

Apuntes adquiridos en clases por el Ing. Raul Bermudez.