La brújula es un instrumento que sirve para orientarse y que su fundamento está basado principalmente en la propiedad de las agujas magnetizadas. A través de una aguja imantada se señala el norte magnético, el cual es ligeramente diferente en cada zona del planeta. También es diferente al norte geográfico.
La aguja imantada indica la dirección del campo magnético terrestre, apuntando hacia el polo norte y polo sur.
Como nota curiosa, hay que decir que solo hay dos zonas del mundo donde no es útil, en los polos. La razón es la convergencia de las líneas de fuerza que tiene el campo magnético terrestre.
- Partes de la Brújula
Los aparatos utilizados para mediciones angulares están: la brújula y el teodolito. por eso en los levantamientos topográficos las observaciones angulares pueden estar referidas a una línea fija.
Diferentes tipos de brújula
- Brújula de Bolsillo: son las que generalmente se sostienen con la mano.
- Brújula de Topografía: se monta sobre un trípode liviano o algunas veces en un bastón.
- Brújula de Tránsito: Se monta sobre la placa superior del aparato.
Brújula de Geólogo
Es un instrumento básico de orientación en campo bastante utilizado en Ingeniería Geológica, Ingeniería de Minas e Ingeniería Civil, con este equipo podemos determinar ángulos azimutales o rumbales (con lo que se establece el ángulo horizontal), medir ángulos verticales o el porcentaje de gradiente (o pendiente), hallar planos horizontales y comprobar la inclinación de los objetos.
Muy usado para determinar el Rumbo y buzamiento de los estratos, fallas y diaclasas, inclinación de estructuras geológicas, también podemos determinar el rumbo de las galerías en minas, la inclinación de las mismas.
Toda observación angular puede estar referida a una línea fija, esta línea puede ser una cualquiera del levantamiento o una fija puramente imaginaria a la que se denomina meridiano convencional. si dicha line pasa efectivamente por los polos norte y sur de la tierra, es decir se tiene orientación norte – sur y se llama “ meridiano verdaderos( geográfico).
VARIACIONES DE LA DECLINACIÓN MAGNÉTICA
Si la línea pasa por los polos magnéticos se
denomina meridiano magnético. el ángulo que forma la aguja entre el meridiano
magnético y meridiano verdadero se llama “
Declinación Magnética
La declinación cambia constantemente y en un
mismo lugar sufre variaciones que pueden ser: diurnas, anuales, seculares o
irregulares.
- Variación Diurna: consiste en un cambio en ciertas épocas del año y tiene su valor medio cerca de las 10 horas a las 17 horas.
- Variación Anual: consiste en un cambio cíclico de la declinación media de una época del año a otra, pero es muy y que generalmente es de 1 minuto.
- Variación Secular: consiste en un cambio constante de la declinación que hace que ésta aumente o disminuye cada año cierta cantidad.
- Variación Irregular: se debe a perturbaciones magnéticas y lo más probable es que se produzca en tormentas eléctricas o magnéticas.
- Atracción Magnética Local. se puede detectar tomando los rumbos de una alineación en sus dos extremos. si los rumbos tienen el mismo valor angular se puede decir que no hay atracción magnética local y si son diferente existe atracción magnética local y si es necesario hallar el rumbo correcto.
ÁNGULOS Y DIRECCIONES
Una de las
finalidades de la topografía es la localización de puntos sobre la superficie
terrestre, lo cual se logra si se conocen:
- La dirección y la distancia a partir de un punto conocido.
- La dirección desde dos puntos cocidos.
- La distancia desde puntos conocidos.
- La dirección desde un punto y la distancia desde otro punto ambos igualmente conocidos desde otro punto.
- Ángulo Horizontal: Es aquel ángulo cuyos lados se encuentran sobre un plano horizontal.
- Dirección De Una Línea: Es el ángulo horizontal que hay entre una línea y otra que se toma como referencia.
- Ángulo Vertical: Es aquel ángulo cuyos lados se encuentran sobre un plano vertical.
- Pendiente De Una Línea: Es aquel ángulo vertical, de elevación o de depresión que hace una línea con la horizontal.
FORMA DE
MEDICIÓN DE LA DIRECCIÓN DE UNA LÍNEA
De acuerdo
a lo anterior las direcciones entre rectas que unen puntos sobre el terreno se
pueden obtener de varias formas:
- Midiendo los ángulos que hay entre rectas adyacentes.
- Midiendo entre rectas no adyacentes sumando los ángulos que intervienen.
- Midiendo el ángulo que hay desde una línea que se toma como referencia
CLASES
DE MERIDIANOS
- MERIDIANO VERDADERO O GEOGRÁFICO:
Es la recta
imaginaria que une los polos geográficos Norte y Sur, los cuales son
determinados por medio de observaciones astronómicas y donde para cada punto
localizado sobre la superficie terrestre tiene siempre la misma dirección. Esta
línea imaginaria es utilizada como referencia para realizar la ubicación de
cualquier línea que se encuentre sobre la superficie de la tierra.
- MERIDIANO MAGNÉTICO:
Es la línea
imaginaria que une los polos magnéticos de la tierra Norte y Sur, los cuales se
determinan por medio de la brújula, no son paralelos a los meridianos
verdaderos, pues los polos magnéticos se encuentran separados de los polos
geográficos. No poseen una dirección definida, pues los polos magnéticos están
en constante movimiento. Esta línea imaginaria también es utilizada como
referencia para realizar la ubicación de cualquier línea que se encuentre sobre
la superficie de la tierra que se encuentre sobre la superficie de la tierra.
- MERIDIANO ARBITRARIO:
Es una
recta imaginaria, que se toma de forma arbitraria, arbitraria, a partir de la
cual se inicia la lectura de los ángulos requeridos para la localización de un
punto o para la realización de un levantamiento topográfico. Es de mucha
utilidad en levantamientos en los cuales no se conoce la dirección de los
meridianos geográficos o magnéticos, pero en donde su determinación es
indispensable para la ubicación del objeto levantado dentro de un plano objeto
levantado, dentro de un plano.
RUMBO
El rumbo de
una recta es la dirección que ésta tiene con respecto al meridiano que se ha
escogido como referencia y puede definirse como su rumbo así: Verdadero, Magnético, Supuesto.
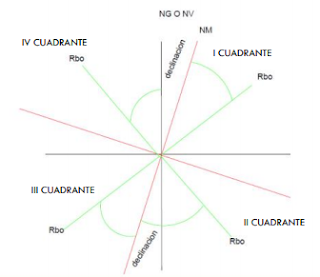
LOS RUMBOS
El rumbo de una línea se indica por el cuadrante en que se encuentra y del ángulo “agudo” que la línea hace con el meridiano en ese cuadrante. en todo los casos los valores de los rumbos están comprendidas entre 0° y 90°. Si un rumbo se encuentra en el norte o sur su valor es de 0° y se llama Norte Franco o Sur Franco.
CONSIDERACIONES CON RELACIÓN A LOS RUMBOS
- El rumbo magnético define del rumbo verdadero por el aumento de la declinación.
- Los rumbos son contados desde los puntos norte o sur y nunca del este u oeste.
- Cada rumbo se designa por dos letras, la primera debe ser n o s. la segunda e o w.
- Nunca un rumbo sobrepasa los 90°
- Toda línea tiene dos rumbos el de adelante y el de espalda, los cuales son numéricamente iguales, pero de letras o puestas.
AZIMUT
Es el
ángulo de una línea en su dirección dada por el ángulo entre el meridiano y la
línea medida en la dirección del movimiento de las manecillas del reloj,
generalmente del norte.
Conversiones
Que Se Deben Tenerse En Cuenta Con Relación A Los Azimut.
Los azimuts se miden a partir del norte.
Se miden únicamente en la dirección de las agujas del reloj.
Está comprendido entre 0° y 360°
El azimut delantero es igual al azimut trasero más 180° y viceversa.
Conversión de azimut a rumbos y viceversa
(Teoría para realizar el ejercicio)
- El azimut comprendido entre 0° y 90° el rumbo tiene el mismo valor.
- Azimut comprendido entre 90° y 180° el rumbo será igual a 180° menos el azimut. Rbo = 180° - az
- azimut comprendido entre 180° y 270° el rumbo será igual : rbo = az – 180°
- azimut comprendido entre 270° y 360° el rumbo será igual a : rbo = 360° - az
Conversión de azimut a rumbos y viceversa
- El azimut comprendido entre 0° y 90° el rumbo tiene el mismo valor.
- Azimut comprendido entre 90° y 180° el rumbo será igual a 180° menos el azimut. Rbo = 180° - az
- Azimut comprendido entre 180° y 270° el rumbo será igual : rbo = az – 180°
- Azimut comprendido entre 270° y 360° el rumbo será igual a : rbo = 360° - az
Rumbos verdaderos o magnéticos
Los rumbos se llaman verdaderos y magnéticos según el meridiano en el que se encuentre si es verdadero o magnético
Para convertir los rumbos magnéticos a verdaderos o astronómicos, se suman o se restan la declinación al rombo magnético según el cuadrante en que se encuentre.
si está en i y iii cuadrante rbo v = rbo mg +∂
si está en ii y iv cuadrante rbo v = rbo mg -
∂
LEY DE PROPAGACIÓN DE LOS AZIMUT
CRITERIOS PARA UTILIZAR LA ECUACIÓN SON:
ØI−1+ < 𝑣𝑒𝑟𝑡𝑖𝑐𝑒 < 180° SE SUMA 180°
LEVANTAMIENTO DE UN TERRENO CON BRUJULA Y CINTA
Se emplean los siguientes métodos: por
radiación y por poligonales.
MÉTODO POR RADIACIÓN
Las condiciones que se siguen para utilizar
este método es que de un vértice central se puedan visualizar todos los
vértices de la poligonal que pueden estar dentro o fuera del polígono. Se
emplea para terrenos pequeños que no tienen interferencia para visualizar cada
uno de los vértices.
ejemplo de cómo anotar los datos obtenidos por este método:
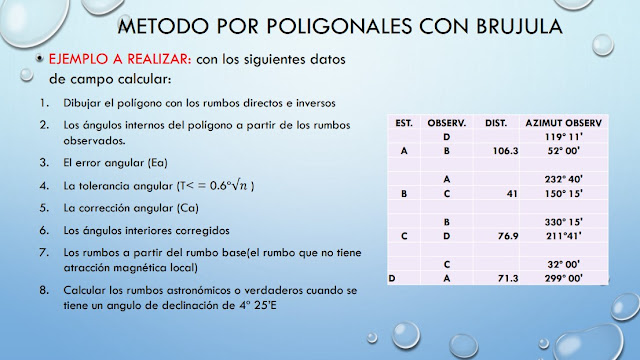
MÉTODO POR POLIGONALES
Reconocimiento del terreno
- En cada vértice hay que tomar datos de los azimut directo e inversos, luego se obtienen los rumbos.
- Entre cada vértice se tiene que tomar las distancias.
- Por diferencia de rumbos se obtienen los ángulos internos los cuales sumados se comparan con ∑≺ 𝑖𝑛𝑡.= 180º(𝑛 − 2)
- Comparar la diferencia de error con la especificaciones donde 𝑇 = 𝑎 𝑛 donde : a: aproximación del aparato= 0.5º= 30’ n= numero de vértices.
- Si el error es menor que la tolerancia se procede a comparar proporcionalmente los ángulos internos y si es mayor tiene que repetirse el levantamiento.
- Lecturas de los azimut mal leídas
- Agujas lenta o dormida(por falta de uso)
- Lectura del extremo incorrecta de la aguja.
- Ajustar la declinación al lado incorrecto del norte.
- Error de paralaje.
- No verificar los rumbos directos e inversos.
- No trazar un esquema
- El azimut de 119°11' está comprendido entre 90° y 180° entonces se realiza la siguiente operación Rbo=180°- azimut ; Rbo=180°-119°11'= 60°49' para colocarle la dirección vemos el azimut y está ubicado en el segundo cuadrante que corresponde al Sur-Este entonces sería S60°49'E
- El azimut de 52°00' esta comprendido entre 0° y 90° no se realiza ninguna operación ya que los Rumbos no pueden ser mayor de 90°, su dirección ya que esta ubicado en el primer cuadrante será Norte-Este queda asi N52°00'E
- El azimut de 232°40' esta comprendido entre 180° y 270° se realiza la siguiente operación Rbo=azimut - 180°; Rbo 232°40'-180°=52°40' para asignarle la dirección vemos el azimut que está ubicado en el tercer cuadrante que corresponde al Sur-Oeste(W) queda asi: S52°40'W
- Y así para los demás Azimut
Ada Funes 27 diciembre, 2018 (El Español) Recuperado de Brújula






















Comentarios
Publicar un comentario