DATOS FALTANTES

Problemas Relativos A Datos Faltantes En Poligonales Cerradas

Cuando por algunas razones no haya sido posible tomar en el campo el RUMBO o la LONGITUD de todos los lados de una poligonal cerrada se puede en general calcular el dato que falta ya que no puede ser más de dos (UNA LONGITUD, UNA DIRECCIÓN O AMBAS A LA VEZ). 

Si solo falta un dato se puede hacer una comprobación parcial del trabajo. una vez suplida las cantidades que faltaban se puede calcular las coordenadas y dibujarse la poligonal como si no faltara dato alguno de campo.

Veamos los diferentes problemas que se nos presentan:

1. Falta Rumbo Y Longitud De Un Lado
2. Falta Longitud De 2 Lados Consecutivos
3. Falta Rumbo De 2 Lados Consecutivos
4. Falta Longitud De Un Lado Y El Rumbo Del Lado Consecutivo

• Falta Rumbo y Longitud de un Lado

Calcular las coordenadas de los diferentes vértices de la poligonal a partir de unas coordenadas bases. Ejemplo:

• Falta Longitud De 2 Lados Consecutivos

En este caso y las siguientes, se pueden resolver calculando la longitud y el rumbo de una línea auxiliar entre los puntos extremos conocidos, formando un triángulo dentro del cual se calculan los elementos faltantes, por la ley del seno o ley coseno. Procedimiento: Calcular las coordenadas de los diferentes vértices de la poligonal Por la línea auxiliar 8-1 se puede obtener el rumbo y la longitud de esa línea. Por diferencia entre los rumbos se obtiene los < en los vértices 8,9,1 Por la ley de los SENOS se obtiene las longitudes 8-9 y 9-1 de esta relación se obtienen las distancias faltantes.

• Falta Rumbo De 2 Lados Consecutivos

Calcular las coordenadas de los diferentes vértices de la poligonal a partir de coordenadas bases.

Por la línea auxiliar se puede obtener el rumbo y la longitud de esa línea.

Conocidos la longitud de los tres lados del triángulo calcular los ángulos internos 5, 6, 1 por cualquier fórmula: 

Con los ángulos internos calculados y el rumbo 5- 1 se obtienen los rumbos de 5-6 y 6-1

• Falta Longitud De Un Lado Y El Rumbo Del Lado Consecutivo

Calcular las coordenadas de los puntos a partir de una coordenada base por la línea auxiliar (calcular su Longitud y Rumbo)

Por la diferencia de rumbo de la línea 4-5 y 4-1 se obtiene el Ángulo interno en 5.

Por la ley del seno obtenemos el Ángulo interno en el vértice 5

Por medio del Rb de 4-5 y el ángulo interno en vértice 4-5 e obtiene el Rb 5-1

Por diferencia de 180°se obtiene el ángulo interno en 1
Por ley del seno se obtiene la dist 4-5

Ejercicio:

Primero se dibuja la poligonal:

Encontramos las proyecciones con las coordenadas ya establecidas.

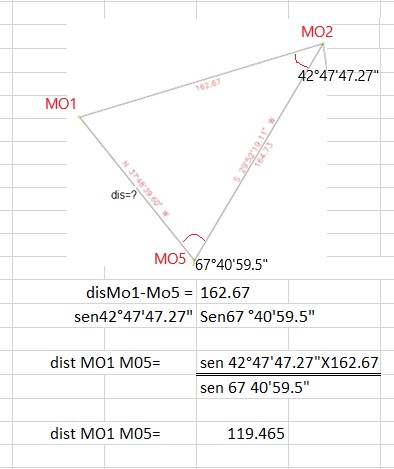
Luego definimos una línea auxiliar de MO2 A MO5 y obtenemos el rumbo y la distancia de esa línea auxiliar.

Lo que me resta es encontrar el rumbo de m01 a m02 con el Ángulo interno del vértice de m01 y el rumbo del vértice mo5 al m01 se obtiene el rumbo de m01 a m02

Para tener la distancia de MO1 a MO5 tengo que tener el ángulo de MO2

Calculando el Ángulo interno en el vértice mo2                                                 

72°40'7.27" -29°52'19.11"=42°47'48.16"=vértice mo2

BIBLIOGRAFÍA

Apuntes adquiridos en clases por el Ing. Raul Bermudez.