ALTIMETRIA

La altimetría se podría definir como una parte de la topografía que se dedica a medir las alturas y estudiar los métodos y técnicas para la representación del relieve de un terreno.

Es fundamental para determinar y representar de la manera más fiel posible la altura o bien cota de cada uno de los puntos respecto al plano de referencia. 

En definitiva, se trata de una rama de la topografía clave para representar, mediante diferentes operaciones matemáticas, la forma y relieve de un terreno. 

Otro concepto.

La altimetría el método topográfico que tiene por objeto determinar las diferencias de alturas entre los puntos de un terreno y posteriormente representar los datos en un plano.

Para conocer esta diferencia de nivel hay que medir distancias Verticales directas o indirectamente, a esta operación se denomina nivelación.

• Directa. Es cuando se mide a partir de un punto
• Indirecta. Cuando se toma de referencia un nivel ya establecido

Datum: se llama a la superficie de nivel que se toma como referencia que puede ser real o imaginaria.

La distancia Verticales que se miden a partir de una superficie de nivel plano o de referencia arbitraria, que debe ser normal o la dirección de la plomada se denomina cota. Cuando el plano de referencia coincide con el nivel del mar, las distribuciones verticales medidas a partir de dicho plano se denomina altitud.

 Dispositivos empleados en una nivelación

 Dentro de los aparatos tenemos desde los más sencillos al más completos:

El aparato más usado es el nivel fijo 

como se utiliza veamos un video Tutorial de Nivel Fijo y Estadía

Para saber a detalle sobre cómo leer la estadía veamos un video Tutoriales. Sobre Leer la Estadía     

Nivelación

Se define como el método de expresar las alturas relativas de varios puntos por encima o por debajo de cierto plano horizontal que se llama plano de referencia (BM)

Banco de marca (BM): se denomina así a un punto más o menos de carácter permanente del cual se conoce su localización y elevación. Nos sirve de base para cualquier nivelación.

Existen cuatro tipos de nivelaciones

1. Nivelación simple
2. Nivelación compuesta
3. Nivelación inversa
4. Nivelación por rasante

Nivelacion simple

Es aquel proceso en el cual desde una sola posición del aparato se puede conocer las cotas de todos los puntos del terreno que se desea nivelar. Las lecturas que intervienen en una nivelación simple son:

• Vista atrás(v.atrás) que se donde se coloca la estadía en mi nivel de referencia llamado BM (Banco de Marca).
• Vista intermedia (V.interm.) es la lectura que se ubica en todos aquellos puntos que deseamos conocer su nivel o elevación.
• Altura de aparato (Alt. de aparato) para conocer la altura de aparato le voy a sumar o la elevación V. atrás. 

Ejemplos 

Nivelacion Compuesta

Es aquella en la cual no es posible visualizar todos los puntos a los cuales se le quiere conocer su elevación siendo necesario trasladar el aparato de posición. El desnivel se obtiene repitiendo una nivelación simple cuantas veces sea necesario, utilizando puntos intermedios llamados puntos de vuelta (puntos de liga, puntos de cambio); la nivelación se va llevando por la ruta mejor posible hasta llegar al punto final.

Ejemplo:

NOTA: Toda nivelación se efectúa a partir de un punto de elevación conocido llamado BANCO DE MARCA

EJEMPLO DE CÁLCULO:

Elevación + vista atrás = altura de aparato 

Altura de aparato - vista adelante = elevación

Elevación + vista atrás = altura de aparato 

Altura de aparato - vista adelante = Elevación.

Nivelación por Rasante

Se debe partir del mismo banco de marca (BM) que se ha realizado la nivelación de dicho proyecto y poder conocer su altura de aparato. Aquí en este proceso se colocará una lectura de mira que es la diferencia entre la altura de aparato y la elevación de la rasante.

Lm = lectura de mira

hA = altura de aparato

Lm = hA - elevacion rasante

 

Comprobación en una nivelación

Para efecto de comprobar que no se ha incurrido en error al efectuar las anotaciones en la libreta o por las operaciones aritméticas se puede establecer que:

Este valor puede ser chequeado por medio de las elevaciones de los puntos

Elev. P.final - Elev. P.inicial  = △ Eleva.

Otra forma de encontrar el error de cierre en nivelación cerrada es por medio de:

TRASLADO DE UN BM A OTRO BM

ERRORES MÁS COMUNES COMETIDOS EN UNA NIVELACIÓN

1. Errores al leer la mira

2. Errores en las anotaciones

3. Errores aritméticos

4. En los puntos de vuelta varían la posición de la vista atrás y vista adelante (procurar hacerlo sobre un punto estable y plano)

5. Que la mira este mal desdoblada.

6. Falta de perpendicularidad en la mira

7. Paralaje. (en enfocar mal el anteojo)

NIVELACIÓN DE UN TERRENO

Dos métodos para poder nivelar un terreno:

1. Sistema por radiación

2. Sistema de cuadrícula

Sistema por radiación

este se utiliza cuando los terrenos no son muy grandes y no tiene obstáculos para que con una sola puesta de aparato se pueda ejecutar la nivelación

Lo que se realiza es una nivelación simple desde un punto del terreno de donde se puedan visualizar todos aquellos puntos y desniveles para poder obtener su respectiva elevación Su forma de anotar. explicar

Cuando se realiza una cuadrícula y el terreno es pequeño se realiza por una nivelación simple asi:

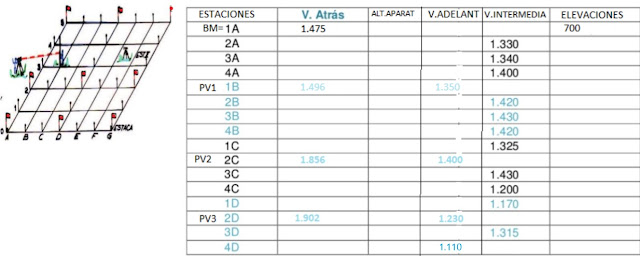
NIVELACIÓN DE UN TERRENO SISTEMA POR CUADRÍCULA

Este se usa cuando el terreno es más extenso y presentan variaciones consideradas de niveles, por eso se utiliza el sistema de cuadrícula para nivelar el terreno.

Anotación de una nivelación compuesta:

CURVAS DE NIVEL

¿Qué es una curva de nivel?  

Es una línea imaginaria que une puntos de igual cota sobre las partes de la superficie terrestre sobre un plano horizontal de referencia. Las curvas de nivel están separadas una de otra por una distancia constante llamadas “x” es una distancia dependiendo del objeto del trabajo se puede espaciar cada 0.5mts,1,2,3,5,10,25 o más o pueden ser menores.

Tomando una serie de planos horizontales equidistantes se obtiene un conjunto de curvas de nivel, las cuales al proyectarse sobre un plano representa el relieve del terreno.

CARACTERÍSTICAS DE LAS CURVAS DE NIVEL

1. Toda curva de nivel se cierra sobre si misma ya sea dentro de la zona considerada o fuera de ella.
2. Toda curva de nivel cerrada le corresponde a una elevación o a una depresión.
3. La distancia horizontal entre 2 curvas de nivel es inversamente proporcional a la pendiente del terreno; así mientras más inclinada sea el terreno más cercano entre sí estarán las curvas de nivel. Cuando la pendiente es uniforme estas serán equidistantes.
4. En superficies planas inclinadas(taludes), las curvas de nivel son rectas y paralelas entre sí.
5. Una curva de nivel va siempre entre una correspondiente a mayor elevación y una correspondiente a menor elevación.
6. Dos curvas de nivel no pueden cortarse
7. Una serie de curvas cerradas concéntricas indican un promontorio o un abismo según la cota vayan creciendo hacia el centro o decreciendo.

MÉTODO DE INTERPOLACIÓN DE LAS CURVAS DE NIVEL

1. Método a estima: se emplea cuando no se requiere mayor precisión y además el dibujante tiene conocimiento del terreno y criterio suficiente para que mediante calculo aproximados mentales puede efectuarse la interpolación.
2. Método Analítico o Matemático: Este método es el que mayor precisión y la interpolación se hace en forma lineal. cuadrícula de 10x10 mts trazar curvas @ 0.5 mts
3. Método Gráfico de interpolación: este método es bastante aproximado y aceptable por estar basado en el teorema de geometría en la división de una recta en tramos iguales.

PERFIL LONGITUDINAL

Se denomina perfil a la línea determinada por la intersección del terreno con un plano vertical. 

Escalas pueden ser:

Vertical: 1:10; 1:100; 1:50; 1:20

Horizontal: 1:100; 1:1000; 1:500; 1:200

Para dibujar el perfil de una línea se necesita conocer las elevaciones y sus respectivos

estacionamientos, estos dos datos se convierten en un sistema de coordenadas en las cuales las abscisas (x) representa la distribución horizontal las ordenadas (y) corresponden a las elevaciones. Uniendo estos puntos determinados se obtiene el perfil de cualquier línea el cual necesitamos realizar con un determinado proyecto.

Aplicaciones de un perfil:

• En una calle o construcción de ella  
• Tuberías de aguas lluvias o negras  
• Apertura de un camino  

Datos adicionales de un perfil:

1. Cota de Corte o Relleno
2. Elevación de corte: elevación TN – Elev Ras
3. Elevación de relleno: Elev Ras – Elev TN
4. Elevación de la rasante

NIVELACIÓN DE UNA FRANJA DE TERRENO

Para poder obtener un perfil longitudinal y transversal (secciones transversales) 

1. Cuando se trata de nivelar una franja de terreno ya sea para obtener un perfil longitudinal y los transversales su procedimiento es el siguiente:
2. Se traza una poligonal abierta a lo largo de la zona cuya topografía se desea conocer
3. Se colocarán trompos en los vértices y guines en las estaciones
4. Se nivela con un nivel de precisión toda la poligonal abierta, con lo cual se fijan elevaciones a los vértices estaciones intermedias.
5. En cada vértice o estación se trazan perpendiculares a cada lado de la poligonal dependiendo el ancho de la zona que queremos conocer su configuración.
6. Se nivela cada uno de las secciones transversales con los cuales se determinan las cotas redondas en todos aquellos puntos para luego trazar sus curvas de nivel.
7. En la nivelación de estas transversales bisectrices se pueden emplear niveles de precisión o de mano.                                                                                                            Pero cuando solo queremos conocer la configuración de dicha sección transversal que nos servirán para la construcción de carreteras, canales, etc.

RASANTE

Cálculo de la elevación de la rasante

Para determinar las elevaciones de la rasante tenemos que determinar la pendiente con la pendiente y las distribuciones parciales calculamos el resto de elevaciones.

Elevaciones.conocidas = elevación conoci. + o - pendiente (x dist. ) / 100

Pendiente

es la diferencia de elevación partida por una distribución reconocida por la rasante con respecto a un plano horizontal que pasa por un extremo de ella.

 P = △ ELEV. / DIST. HORIZONTAL x 100

BIBLIOGRAFÍA:

Apuntes adquiridos en clases por el Ing. Raul Bermudez.